This page contains algorithms and reference formulas used in Gamutvision™. The green text is heavily mathematical. The content is similar to the Imatest Colorcheck Appendix.
Color difference (error) formulas
Several Gamutvision displays use color difference metrics to
quantify the perceptual difference between colors. All of these metrics
are based on L*a*b* color space, which was designed to be perceptually
uniform. If it were truly uniform, perceptual color differences could
be determined by the Euclidian distance between colors expressed as
L*a*b* values (CIE 1976 metrics):
ΔE*ab = ( (L*2-L*1)2 + (a*2-a*1)2 + (b*2-b*1)2 )1/2 = (ΔL*2 + Δa*2 + Δb*2 )1/2
We are often interested in differences between color only, omitting luminance.
ΔC*ab = ((a*2-a*1)2 + (b*2-b*1)2 )1/2 = (Δa*2 + Δb*2 )1/2
However, L*a*b* (sometimes referred to as CIE 1976) is not nearly as
uniform as its designers intended. In particular, the eye is a good
deal less sensitive to differences in chroma (c* = (a*2 + b*2 )1/2 ; i.e., intensity of color) for strongly chromatic colors than it is to hues (hue angle = h* = arctan(b/a) ). To correct this deficiency several color metric formulas have been proposed.
- CIE 1994: ΔE*94 , which includes Luminance L*, and ΔC*94 , which omits L*.
- CMC: ΔE*CMC , which includes Luminance L*, and ΔC*CMC , which omits L*. Widely used in the textile industry for matching bolts of cloth.
- CIEDE2000: ΔE00 , which includes Luminance L*, and ΔC00 , which omits L*.
This is the emerging standard as well as the most accurate color
difference metric. Its acceptance has been slowed by the complexity of
its formula. Although it is less familiar that the other equations, it
is the best choice in the long run.
Whichever metric you choose, remember that they give different
numbers. It is important to be consistent and always specify which
measurement you are using.
The Hue and Chroma differences, ΔH* and ΔC*, are of interest for their own sake and because they are used in the CIE 1994 and CMC color difference formulas, below.
ΔH* = ( (ΔE*ab )2 - (ΔL*)2 - (ΔC*)2 )1/2 (Hue difference ; DCIH (5.36) )
Δc* = ( a1*2 + b1*2 )1/2 – ( a2*2 + b2*2 )1/2 (Chroma difference)
Δh* = 180/π (arctan( b1* / a1*) – arctan( b2* / a2*) ) (Hue angle difference ; see online Errata )
Δh* = Δh* - 360 if Δh* > 200 ; Δh* = Δh* + 360 if Δh* < -200
Δh* = 0 where the hue angle is poorly defined: L* < 2 ; max(a1 , b1*) < 2 ; max(a2 , b2*) < 2 ;
Now for the math...
The notation in this section is adapted from the Digital Color Imaging Handbook, edited by Gaurav Sharma, published by the CRC Press, referred to below as DCIH. The DCIH online Errata was consulted.
Absolute differences (including luminance)
CIE 1976
The L*a*b* color space was designed to be relatively
perceptually uniform. That means that perceptible color difference is
approximately equal to the Euclidean distance between L*a*b* values.
For colors {L1*, a1*, b1*} and {L2*, a2*, b2*}, where ΔL* = L2* - L1*, Δa* = a2* - a1*, and Δb* = b2* - b1*,
ΔE*ab = ( ( ΔL*)2 + (Δa*)2 + (Δb*)2 )1/2 (DCIH (1.42, 5.35); (...)1/2 denotes square root of (...) ).
Although ΔE*ab
is relatively simple to calculate and understand, it's not very
accurate especially for strongly saturated colors. L*a*b* is not as
perceptually uniform as its designers intended. For example, for
saturated colors, which have large chroma values (C* = ( a*2 + b*2 )1/2 ), the eye is less sensitive to changes in chroma than to corresponding changes for Hue (ΔH* = ( (ΔE*ab)2 - (ΔL*)2 - (ΔC*)2 )1/2 ) or Luminance (ΔL*). To
address this issue, several additional color difference formulas have
been established. In these formulas, just-noticeable differences (JNDs)
are represented by ellipsoids rather than circles.
CIE 1994
The CIE-94 color difference formula, ΔE*94, provides a better measure of perceived color difference.
ΔE*94 = ( (ΔL*)2 + (ΔC*/SC )2 + (ΔH*/SH )2 )1/2 (DCIH (5.37); omitting constants set to 1 ), where
SC = 1 + 0.045 C* ; SH = 1 + 0.015 C* (DCIH (1.53, 1.54) )
[ C* = ( ( a1*2 + b1*2 )1/2 ( a2*2 + b2*2 )1/2 )1/2
(the geometrical mean chroma) gives symmetrical results for colors 1
and 2. However, when one of the colors (denoted by subscript s) is the standard, the chroma of the standard, Cs* = ( as*2 + bs*2 )1/2, is preferred for calculating SC and SH. The asymmetrical equation is used by Bruce Lindbloom.]
An early meeting of the
CMC Standards Committee
CMC
The
CMC color difference formula is widely used by the textile industry to
match bolts of cloth. Although it's less familiar to photographers than
the CIE 1976 geometric distance ΔE*ab , it's probably the best of the measurement metrics. It is slightly asymmetrical: subscript s denotes the standard (reference) measurement. CMC is the Colour Measurement Committee of the Society of Dyers and Colourists (UK). |
 |
ΔE*CMC(l,c) = ( (ΔL*/lSL)2 + (ΔC*/cSC )2 + (ΔH*/SH )2 )1/2 (DCIH (5.37) ), where
(That's the lowercase letter l in (l,c) and the denominator of (ΔL*/lSL)2.) ΔE*CMC(1,1) (l = c = 1) is used for graphic arts perceptibility measurements. l = 2 is used in the textile industry for acceptability of fabric matching. For now Imatest displays ΔE*CMC(1,1).
SL = 0.040975 Ls* / (1+0.01765 Ls*) ; Ls* ≥ 16 (DCIH (1.48) )
= 0.511 ; Ls* < 16
SC = 0.0638 cs* / (1+0.0131 cs* ) + 0.638 ; SH = SC (TCMC FCMC + 1 - FCMC ) (DCIH (1.49, 1.50) )
FCMC = ( ( cs*)4 / ( ( cs*)4 + 1900 ) )1/2 (DCIH (1.51);
TCMC = 0.56 + | 0.2 cos(hs* + 168°) | 164° ≤ hs* ≤ 345° (DCIH (1.52) )
= 0.36 + | 0.4 cos(hs* + 35 °) | otherwise
CIEDE2000
The CIEDE2000 formulas (ΔEoo and ΔCoo
) are the upcoming standard, and may be regarded as more accurate than
the previous formulas. We omit the equations here because they are
described very well on Gaurav Sharma's CIEDE2000 Color-Difference Formula web page. Default values of 1 are used for parameters kL, kC, and kH.
At the time of this writing (February 2008) the CIE 1976 color difference metrics (ΔE*ab...) are still the most familiar. CIE 1994 is more accurate and robust, and retains a relatively simple equation. ΔE*CMC is more complex but widely used in the textile industry. The complexity of the CIEDE2000 equations
(DCIH, section 1.7.4, pp. 34-40) has slowed their widespread adoption,
but they are on their way to becomming the accepted standard. For the long run, CIEDE2000 color difference metrics are the best choice.
Color differences that omit luminance difference
Photographic
papers, especially matte papers, are not able to reproduce deep gray
and black tones well. This results in a large density difference that
has a strong effect on ΔE*ab, ΔE*94, and ΔE*94. It can be useful to look at color errors independently of density error. Color differences that omit ΔL* include
ΔC*ab = ((Δa*)2 + (Δb*)2 )1/2
ΔC*94 = ( (Δc*/SC )2 + (ΔH*/SH )2 )1/2
ΔC*CMC = ((Δc*/SC )2 + (ΔH*/SH )2 )1/2
These formulas don't entirely remove the effects of exposure error since L* is affected by exposure, but they reduce it to a manageable level.
Gamut volume algorithm
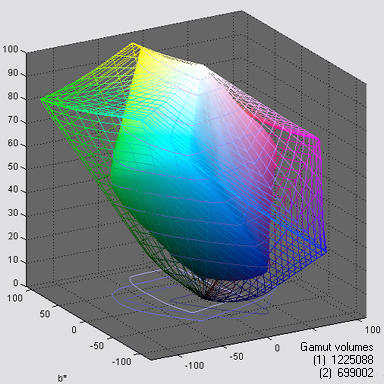 L*a*b*
Gamut volume is the best single number for characterizing the color
response of a device or color space profile. L*a*b* gamuts and volumes
are shown on the right for Adobe RGB (1998) color space (wireframe) and
the Epson R2400, Premium Luster (solid), mapped from Adobe RGB with
perceptual rendering intent. The units of L*a*b* volume are sometimes
labelled ΔE3 (referring to ΔE*ab, above).
L*a*b*
Gamut volume is the best single number for characterizing the color
response of a device or color space profile. L*a*b* gamuts and volumes
are shown on the right for Adobe RGB (1998) color space (wireframe) and
the Epson R2400, Premium Luster (solid), mapped from Adobe RGB with
perceptual rendering intent. The units of L*a*b* volume are sometimes
labelled ΔE3 (referring to ΔE*ab, above).
Gamut volume is not easy to calculate: it can't be directly
extracted from the profile. The Gamutvision algorithm calculates the
gamut volume from an image containing all values of HSL Hue H and Lightness L for a fixed value of Saturation S (usually the maximum value, S = 1), illustrated below (on the right) and in Gamutvision Structure (on the left). This image is used to generate the gamuts on the right. The algorithm is as follows.
- Map the RGB image values into L*a*b*.
- Find the "center of mass" of the gamut. This is typically in the neighborhood of L* = 55, a* = b* = 0.
- Convert the values into cylindrical coordinates (R, Θ, Φ) with origin at the center of mass.
- Create a "binning" array representing uniformly spaced longitudinal and latitudinal angles (Θ and Φ, spaced δΘ and δΦ).
- Place the average radius (R) corresponding to each image point in the appropriate binning array element.
- Interpolate to fill the missing points.
- Sum the volumes for each array entry to find the total volume V = ∑δV, where
δV = R2 δh δΘ / 3 ; δh = R cos(Φ) δΦ ; δV = R3 cos(Φ) δΘ δΦ / 3 (ΔE3 units)
The color space gamuts calculated by this algorithm are about 1% higher than than the volumes reported by Bruce Lindbloom,
except for extremely large gamut spaces (ProPhoto, WideGamut) which
contain a* and b* values larger than the Gamutvision limits of ±128.
Light and Color
This section reviews the basic concepts of additive and subtractive
color. If you are familiar with them, you may want to skip to Color models section, below. Color theory is dealt with in more depth in the series on Color management.
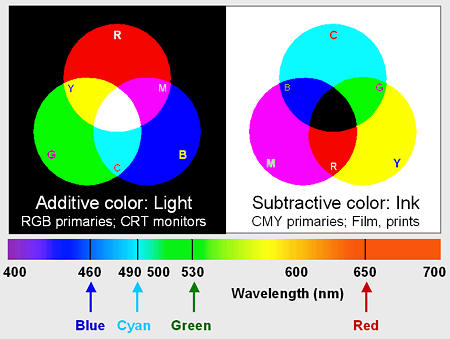 The
human eye is sensitive to electromagnetic radiation with wavelengths
between about 380 and 700 nanometers. This radiation is known as light. The visible spectrum is illustrated on the right. The eye has three classes of color-sensitive light receptors called cones,
which respond roughly to red, blue and green light (around 650, 530 and
460 nm, respectively). A range of colors can be reproduced by one of
two complimentary approaches:
The
human eye is sensitive to electromagnetic radiation with wavelengths
between about 380 and 700 nanometers. This radiation is known as light. The visible spectrum is illustrated on the right. The eye has three classes of color-sensitive light receptors called cones,
which respond roughly to red, blue and green light (around 650, 530 and
460 nm, respectively). A range of colors can be reproduced by one of
two complimentary approaches:
- Additive color: Combine light sources, starting with darkness (black). The additive primary
colors are red (R), green (G), and blue (B). Adding R and G light makes
yellow (Y). Similarly, G + B = cyan (C) and R + B = magenta (M).
Combining all three additive primaries makes white.
- Subtractive color: Illuminate objects that contain dyes or pigments that remove
portions of the visible spectrum. The objects may either transmit light
(transparencies) or reflect light (paper, for example). The subtractive primaries
are C, M and Y. Cyan absorbs red; hence C is sometimes called "minus
red" (-R). Similarly, M is -G and Y is -B. The two approaches are
illustrated on the right and described in the table below.
Unfortunately, ideal C, Y and M inks don't exist; the subtractive
primaries don't entirely remove their compliments (R, B and G). This
isn't a problem for film, where light is transmitted through three
separate dye layers, but it has important consequences for prints made
with ink on reflective media (i.e., paper). Combining C, Y and M
usually produces a muddy brown. Black ink (K) must added to the mix to
obtain deep black tones. CMYK color is highly device dependent-- there
are many algorithms for converting RGB to CMYK. Photographic editing
should be done in RGB) color spaces. Conversion to CMYK (usually with
colors added to extend the printer color gamut) should be left to the
printer driver software.
| Additive color |
Subtractive color |
| Light sources: beams of light or dots of light on monitor screens |
Objects that transmit or reflect light: film or prints. Typically illuminated by white light. |
| Primaries: Red (R), Green (G), Blue (B) |
Primaries: Cyan (C), Magenta (M), Yellow (Y) |
| Light from independent sources is added. |
Portions
of the visible light spectrum are absorbed by inks, which contain dyes
or pigments, or by dye layers in photographic film or paper. |
| Adding
red and green makes yellow (R + G = Y); Similarly, G + B = C and R + B
= M. Adding all three additive primaries in roughly equal amounts
creates gray or white light. |
Each
subtractive primary removes one of the additive primary colors from the
reflected or transmitted image. Cyan (C) removes red; hence it is known
as minus red (-R). Similarly, M is -G and Y is -B. Objects are
typically illuminated by white light. Combining two subtractive
primaries makes an additive primary (see illustration). Combining all
three subtractive primaries in roughly equal amounts creates gray or
black. |
|
You can obtain a wide range of colors, but not all the colors the eye can see, by combining RGB light. The gamut
of colors a device can reproduce depends on the spectrum of the
primaries, which can be far from ideal. To complicate matters, the
eye's response doesn't correspond exactly to R, G and B, as
commonly defined (the description above is oversimplified). Device
color gamut and the eye's response are discussed in detail in the page
on Color Management.
Color models
If you lighten or darken color images you need to understand how
color is represented. Unfortunately there are several models for
representing color. The first two should be familiar; the latter two
may be new.
- RGB - Red, Green, Blue; The additive
primary colors. Used for monitor screens and most image file formats.
There are actually a number of RGB color spaces--
sRBG, Adobe RGB 1998, Bruce RGB, Chrome 2000, etc.-- differing from
each other in the purity of their primary colors, which affects their gamut-- they range of colors they represent. They are discussed in Color Management.
- CMY(K)
- Cyan, Magenta, Yellow; The subtractive primary colors: the
compliments of the additive primaries (Cyan is -red; magenta is -green;
yellow is -blue.) Widely used in inks for printing with black (K)
added because C, M, and Y pigments and inks rarely give deep, rich
black tones by themselves (they tend to make a muddy brown). CMYK is
important to the prepress industry, but most photographers don't need
to be concerned with it. Most high quality photographic printers have
additional inks (light M, light C and gray may be added to the basic
four), so they aren't really CMYK; the printer driver software converts
RGB files into ink densities.
- HSV - Hue,
Saturation, Value. Hue is what we perceive as color. S is saturation:
100% is a pure color. 0% is a shade of gray. Value is related to
brightness. HSV and HSL (below) are obtained by mathematically
transforming RGB. HSV is the identical to HSB.
- HSL - Hue, Saturation, Lightness. H is the same as in HSV but L and V are defined differently. S is similar for dark colors but quite different for light colors. Also called HLS.
It is not practical to use RGB or CMY(K) to adjust brightness or
color saturation because each of the three color channels would have to
be changed, and changing them by the same amount to adjust brightness
would usually shift the color (hue). HSV and HSL are practical for
editing because the software only needs to change V, L, or S. Image
editing software typically transforms RGB data into one of these
representations, performs the adjustment, then transforms the data back
to RGB. You need to know which color model is used because the effects
on saturation are very different.
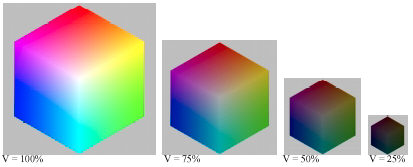
HSV color is shown here in an illustration from Jonathan Sachs' tutorial, "The Basics of Digital Images" (right click on the link to save it in Adobe PDF format). V = max(R,G,B). Maximum Value (V = 1 or 100%) corresponds to pure white (R=G=B=1) and to any fully saturated color (at least one RGB value at 1 and one at 0; no gray component (W = min(R,G,B)). V = 0 is pure black, regardless of H and S. The HSV color model can be depicted as a cone, widest at the top (V = 1), coming to a point at the bottom (V
= 0; pure black). (I use the "V"-like appearance of the cone as a
mnemonic to remember "HSV." The names of the color models are pretty
arbitrary.) efg has a technically detailed explanation of the HSV color model, complete with a Java applet. |
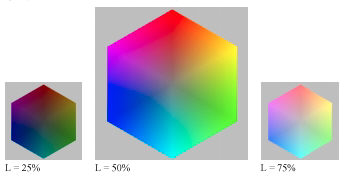
 |
HSL color. Maximum color saturation takes place at L = 0.5 (50%). L = 0 is pure black and L = 1 (100%) is pure white, regardless of H or S. The HSL color model can be depicted as a double cone, widest at the middle (L = 0.5), coming to points at the top (L = 1; pure white) and bottom (L = 0; pure black). |
 |
Now the important part. What you must remember about the HSV and HSL color models is,
| |
Darkening in HSV reduces saturation. |
|
Darkening in HSL increases saturation when L > 0.5. |
|
| |
Lightening in HSV increases saturation. |
|
Lightening in HSL reduces saturation when L > 0.5. |
|
| |
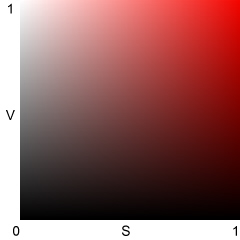
HSV
Best representation of saturation |
|
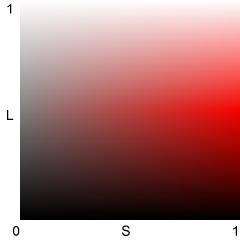
HSL
Best representation of lightness |
|
HSV and HSL were developed to represent colors in systems with
limited dynamic range (pixel levels 0-255 for 24-bit color). The
limitation forces a compromise. HSV represents saturation much better
than brightness: V = 1 can be a pure primary color or pure
white; hence "Value" is a poor representation of brightness. HSL
represents brightness much better than saturation: L = 1 is always pure white, but when L > 0.5, colors with S = 1 contain white, hence aren't completely saturated. In both models, hue H is unchanged when L, V, or S are adjusted.
HSV and HSL are illustrated above for red (H = 0). S varies from 0 to 1 along the horizontal axis; V and L vary from 0 to 1 along the vertical axis. The right side of the HSV illustration (S = 1) always has maximum saturation (G = B = 0) but the top (V = 1) varies from pure white at S = 0 to pure red at S = 1. The top of the HSL illustration (L = 1) is pure white for all values of S. It would be nice to be able to represent brightness and saturation properly in one system, but you can't have it both ways.
HSV and HSL equations
Hue H is the same for HSV and HSL. The full equations are in efg's HSV lab report. Expressed in degrees (0-360º) for any nonzero x, H = 0 for Red (x,0,0); 60º for Yellow (x,x,0), 120º for Green (0,x,0) (illustrated below), 180º for Cyan (0,x,x), 240º for Blue (0,0,x), and 300º for Magenta (x,0,x). H can also be represented on a scale of 0 to 1.
Assume R, G, and B can have values between 0 and 1. Let W = min(R,G,B) = the gray component.
|
HSV (HSB)
|
HSL (HLS)
|
|
V = max(R,G,B)
|
L = (V+W)/2
|
|
SHSV = (V-W) / V
|
SHSL = (V-W) / (V+W) = (V-W) / (2L) ; L <= 0.5
SHSL = (V-W) / (2-V-W) = (V-W) / (2-2L) ; L > 0.5
|
Any color with R, G, or B = 1 has V = 1.
Maximum saturation occurs when W = 0.
|
A bright, fully saturated color (max(R,G,B) = V = 1; min(R,G,B) = W = 0; SHSV = SHSL = 1) must have L = 0.5. L = 1 corresponds to pure white.
|
|
V, L, and S illustrated for H = 0.333 (120º; Green)
|
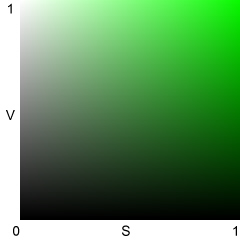
HSV: Best representation of saturation
|
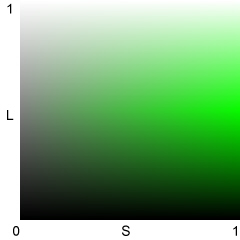
HSL: Best representation of lightness
|
|
V, L, and H illustrated for S = 1 (maximum saturation)
|
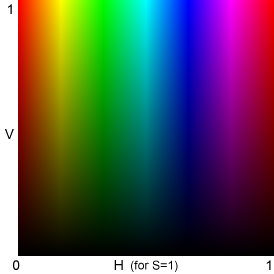
HSV: identical to the bottom half
of the HSL pattern on the right
|
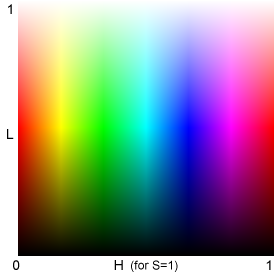
HSL: used for 3D L*a*b* gamut display
and
gamut volume calculation
|
| The Y, C, and M bands are much narrower than the R, G, and B bands. Y, C, and M appear brighter than R, G, and B at similar V and L levels because both V and L are related to max(R,G,B).
|
Some interesting relationships
(1) For W = min(R,G,B) = 0 (no gray; maximum saturation), SHSL = SHSV = 1 ; L = V / 2 ; L <= 0.5.
(2) For V = max(R,G,B) = 1 and SHSL = 1, L = 1-(SHSV / 2) ; SHSV = (1-L) / 2; L >= 0.5
|
|
These relationships imply that (1) the bottom half of the HSL L-H plot for S = 1 (above, right) is identical to the HSV V-H plot for S = 1 (above, left), and (2) the top half of the HSL S-H plot is identical to an HSV S-H plot for V=1 (not shown), i.e., the HSL L-H plot (above, right) combines two HSV plots.
|
All saturation equations have V-W in the numerator; they differ in denominator scaling. In both representations, S is a measure of relative saturation. S is 0 when W = V (R = G = B; neutral gray); S = 1 when W is at its minimum allowable value for a given value of V or L. For HSV, W = 0 when S = 1.
For HSL with L <= 0.5, maximum saturation takes place when W = 0; SHSL = (V-W) / (V+W) = 1. When L > 0.5, W must be greater than 0. Maximum saturation takes place when W = 2L-V takes its minimum value, Wmin. In this case V = 1, so Wmin = 2L-1. SHSL = (V-W) / (2-V-W) = (1-2L+1) / (2-1-2L+1) = 1.
V and L don't correspond with perceived luminance; for example, blue and gray or white with the same V or L
values would have very different luminance. The PAL luminance signal, Y
= 0.30R + 0.59G + 0.11B, corresponds more closely to perceived
luminance.

 L*a*b*
Gamut volume is the best single number for characterizing the color
response of a device or color space profile. L*a*b* gamuts and volumes
are shown on the right for Adobe RGB (1998) color space (wireframe) and
the Epson R2400, Premium Luster (solid), mapped from Adobe RGB with
perceptual rendering intent. The units of L*a*b* volume are sometimes
labelled ΔE3 (referring to ΔE*ab, above).
L*a*b*
Gamut volume is the best single number for characterizing the color
response of a device or color space profile. L*a*b* gamuts and volumes
are shown on the right for Adobe RGB (1998) color space (wireframe) and
the Epson R2400, Premium Luster (solid), mapped from Adobe RGB with
perceptual rendering intent. The units of L*a*b* volume are sometimes
labelled ΔE3 (referring to ΔE*ab, above).  The
human eye is sensitive to electromagnetic radiation with wavelengths
between about 380 and 700 nanometers. This radiation is known as light. The visible spectrum is illustrated on the right. The eye has three classes of color-sensitive light receptors called cones,
which respond roughly to red, blue and green light (around 650, 530 and
460 nm, respectively). A range of colors can be reproduced by one of
two complimentary approaches:
The
human eye is sensitive to electromagnetic radiation with wavelengths
between about 380 and 700 nanometers. This radiation is known as light. The visible spectrum is illustrated on the right. The eye has three classes of color-sensitive light receptors called cones,
which respond roughly to red, blue and green light (around 650, 530 and
460 nm, respectively). A range of colors can be reproduced by one of
two complimentary approaches: 






